Deep Q-Learning (DQN)
Overview
As an extension of the Q-learning, DQN's main technical contribution is the use of replay buffer and target network, both of which would help improve the stability of the algorithm.
Original papers:
Implemented Variants
| Variants Implemented | Description |
|---|---|
dqn_atari.py, docs |
For playing Atari games. It uses convolutional layers and common atari-based pre-processing techniques. |
dqn.py, docs |
For classic control tasks like CartPole-v1. |
dqn_atari_jax.py, docs |
For playing Atari games. It uses convolutional layers and common atari-based pre-processing techniques. |
dqn_jax.py, docs |
For classic control tasks like CartPole-v1. |
Below are our single-file implementations of DQN:
dqn_atari.py
The dqn_atari.py has the following features:
- For playing Atari games. It uses convolutional layers and common atari-based pre-processing techniques.
- Works with the Atari's pixel
Boxobservation space of shape(210, 160, 3) - Works with the
Discreteaction space
Usage
poetry install --with atari
python cleanrl/dqn_atari.py --env-id BreakoutNoFrameskip-v4
python cleanrl/dqn_atari.py --env-id PongNoFrameskip-v4
Explanation of the logged metrics
Running python cleanrl/dqn_atari.py will automatically record various metrics such as actor or value losses in Tensorboard. Below is the documentation for these metrics:
charts/episodic_return: episodic return of the gamecharts/SPS: number of steps per secondlosses/td_loss: the mean squared error (MSE) between the Q values at timestep \(t\) and the Bellman update target estimated using the reward \(r_t\) and the Q values at timestep \(t+1\), thus minimizing the one-step temporal difference. Formally, it can be expressed by the equation below. $$ J(\theta^{Q}) = \mathbb{E}_{(s,a,r,s') \sim \mathcal{D}} \big[ (Q(s, a) - y)^2 \big], $$ with the Bellman update target is \(y = r + \gamma \, Q^{'}(s', a')\) and the replay buffer is \(\mathcal{D}\).losses/q_values: implemented asqf1(data.observations, data.actions).view(-1), it is the average Q values of the sampled data in the replay buffer; useful when gauging if under or over estimation happens.
Implementation details
dqn_atari.py is based on (Mnih et al., 2015)1 but presents a few implementation differences:
dqn_atari.pyuse slightly different hyperparameters. Specifically,dqn_atari.pyuses the more popular Adam Optimizer with the--learning-rate=1e-4as follows:whereas (Mnih et al., 2015)1 (Exntended Data Table 1) uses the RMSProp optimizer withoptim.Adam(q_network.parameters(), lr=1e-4)--learning-rate=2.5e-4, gradient momentum0.95, squared gradient momentum0.95, and min squared gradient0.01as follows:optim.RMSprop( q_network.parameters(), lr=2.5e-4, momentum=0.95, # ... PyTorch's RMSprop does not directly support # squared gradient momentum and min squared gradient # so we are not sure what to put here. )dqn_atari.pyuses--learning-starts=80000whereas (Mnih et al., 2015)1 (Exntended Data Table 1) uses--learning-starts=50000.dqn_atari.pyuses--target-network-frequency=1000whereas (Mnih et al., 2015)1 (Exntended Data Table 1) uses--learning-starts=10000.dqn_atari.pyuses--total-timesteps=10000000(i.e., 10M timesteps = 40M frames because of frame-skipping) whereas (Mnih et al., 2015)1 uses--total-timesteps=50000000(i.e., 50M timesteps = 200M frames) (See "Training details" under "METHODS" on page 6 and the related source code run_gpu#L32, dqn/train_agent.lua#L81-L82, and dqn/train_agent.lua#L165-L169).dqn_atari.pyuses--end-e=0.01(the final exploration epsilon) whereas (Mnih et al., 2015)1 (Exntended Data Table 1) uses--end-e=0.1.dqn_atari.pyuses--exploration-fraction=0.1whereas (Mnih et al., 2015)1 (Exntended Data Table 1) uses--exploration-fraction=0.02(all corresponds to 250000 steps or 1M frames being the frame that epsilon is annealed to--end-e=0.1).dqn_atari.pyhandles truncation and termination properly like (Mnih et al., 2015)1 by using SB3's replay buffer'shandle_timeout_termination=True.
dqn_atari.pyuse a self-contained evaluation scheme:dqn_atari.pyreports the episodic returns obtained throughout training, whereas (Mnih et al., 2015)1 is trained with--end-e=0.1but reported episodic returns using a separate evaluation process with--end-e=0.01(See "Evaluation procedure" under "METHODS" on page 6).
Experiment results
To run benchmark experiments, see benchmark/dqn.sh. Specifically, execute the following command:
Below are the average episodic returns for dqn_atari.py.
| Environment | dqn_atari.py 10M steps |
(Mnih et al., 2015)1 50M steps | (Hessel et al., 2017, Figure 5)3 |
|---|---|---|---|
| BreakoutNoFrameskip-v4 | 366.928 ± 39.89 | 401.2 ± 26.9 | ~230 at 10M steps, ~300 at 50M steps |
| PongNoFrameskip-v4 | 20.25 ± 0.41 | 18.9 ± 1.3 | ~20 10M steps, ~20 at 50M steps |
| BeamRiderNoFrameskip-v4 | 6673.24 ± 1434.37 | 6846 ± 1619 | ~6000 10M steps, ~7000 at 50M steps |
Note that we save computational time by reducing timesteps from 50M to 10M, but our dqn_atari.py scores the same or higher than (Mnih et al., 2015)1 in 10M steps.
Learning curves:
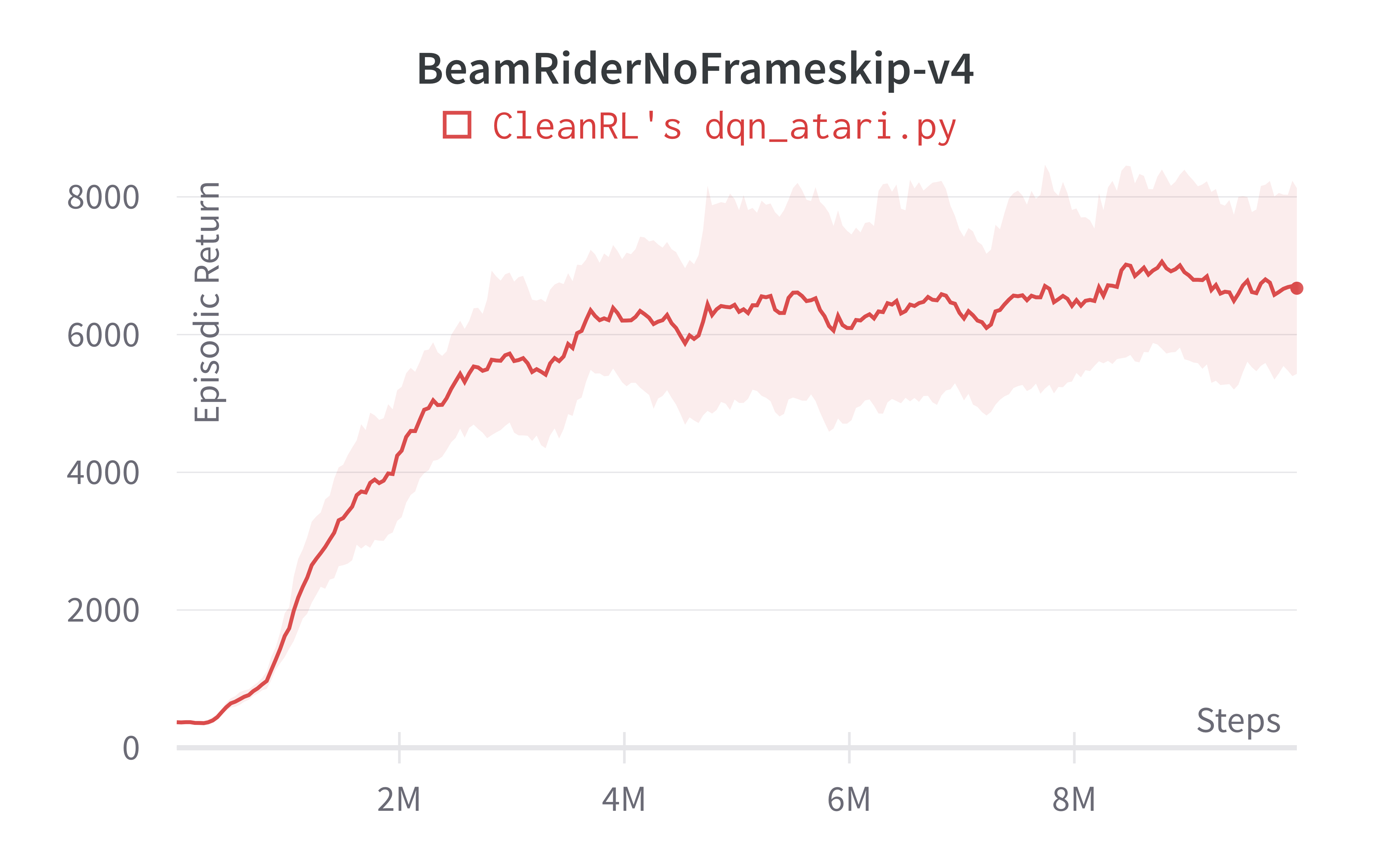
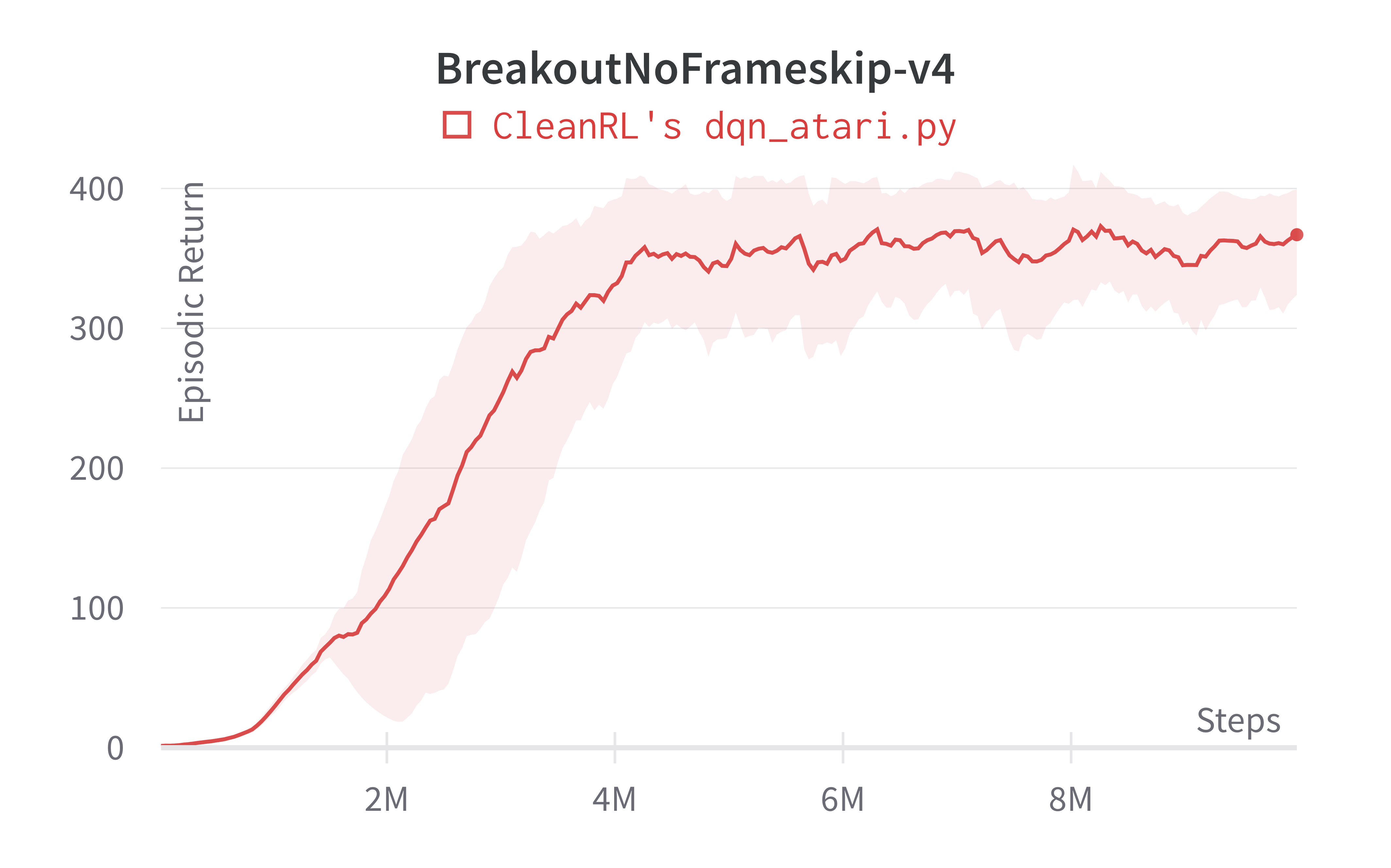
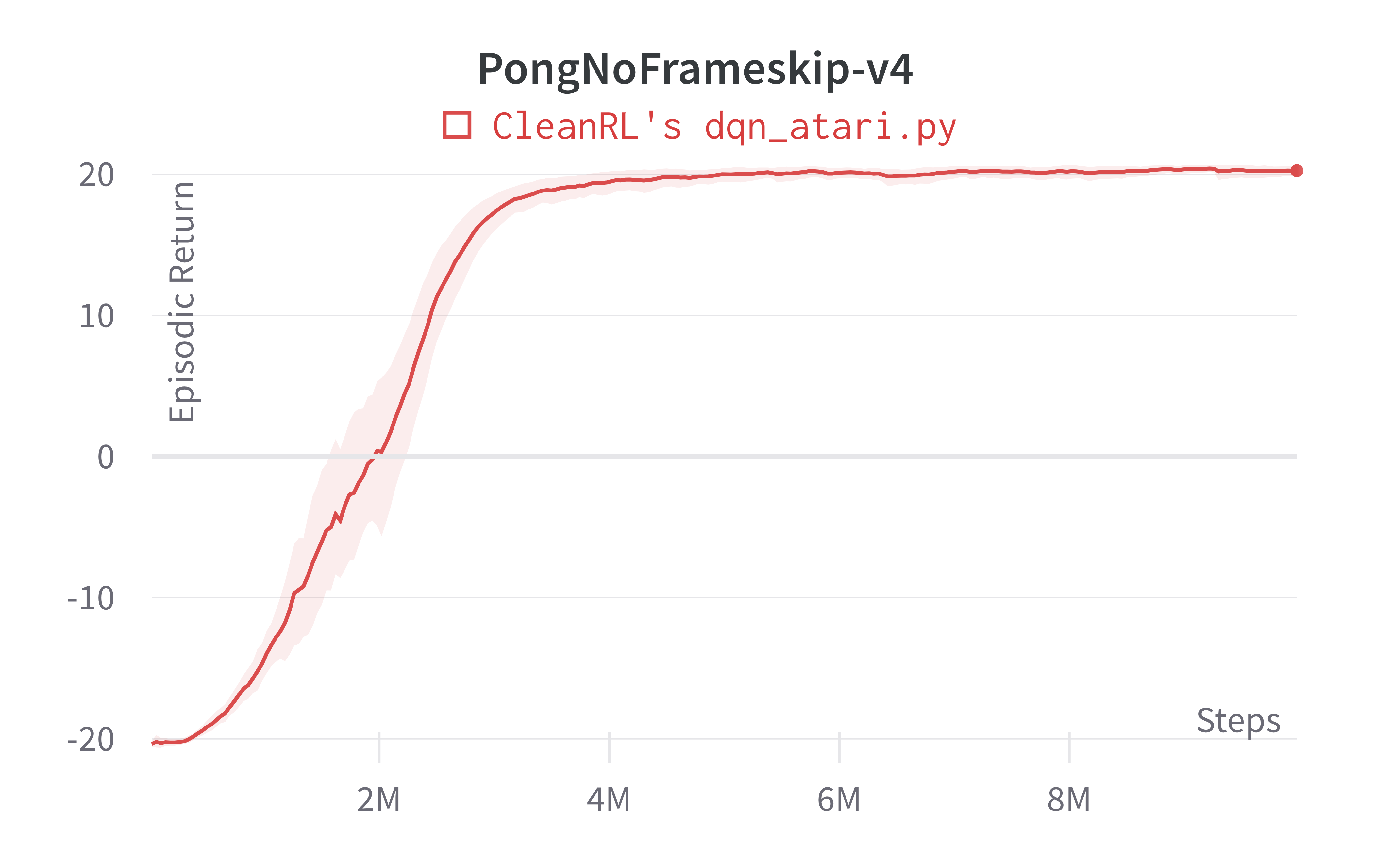
Tracked experiments and game play videos:
dqn.py
The dqn.py has the following features:
- Works with the
Boxobservation space of low-level features - Works with the
Discreteaction space - Works with envs like
CartPole-v1
Usage
python cleanrl/dqn.py --env-id CartPole-v1
Explanation of the logged metrics
See related docs for dqn_atari.py.
Implementation details
The dqn.py shares the same implementation details as dqn_atari.py except the dqn.py runs with different hyperparameters and neural network architecture. Specifically,
dqn.pyuses a simpler neural network as follows:self.network = nn.Sequential( nn.Linear(np.array(env.single_observation_space.shape).prod(), 120), nn.ReLU(), nn.Linear(120, 84), nn.ReLU(), nn.Linear(84, env.single_action_space.n), )-
dqn.pyruns with different hyperparameters:python dqn.py --total-timesteps 500000 \ --learning-rate 2.5e-4 \ --buffer-size 10000 \ --gamma 0.99 \ --target-network-frequency 500 \ --max-grad-norm 0.5 \ --batch-size 128 \ --start-e 1 \ --end-e 0.05 \ --exploration-fraction 0.5 \ --learning-starts 10000 \ --train-frequency 10
Experiment results
To run benchmark experiments, see benchmark/dqn.sh. Specifically, execute the following command:
Below are the average episodic returns for dqn.py.
| Environment | dqn.py |
|---|---|
| CartPole-v1 | 488.69 ± 16.11 |
| Acrobot-v1 | -91.54 ± 7.20 |
| MountainCar-v0 | -194.95 ± 8.48 |
Note that the DQN has no official benchmark on classic control environments, so we did not include a comparison. That said, our dqn.py was able to achieve near perfect scores in CartPole-v1 and Acrobot-v1; further, it can obtain successful runs in the sparse environment MountainCar-v0.
Learning curves:
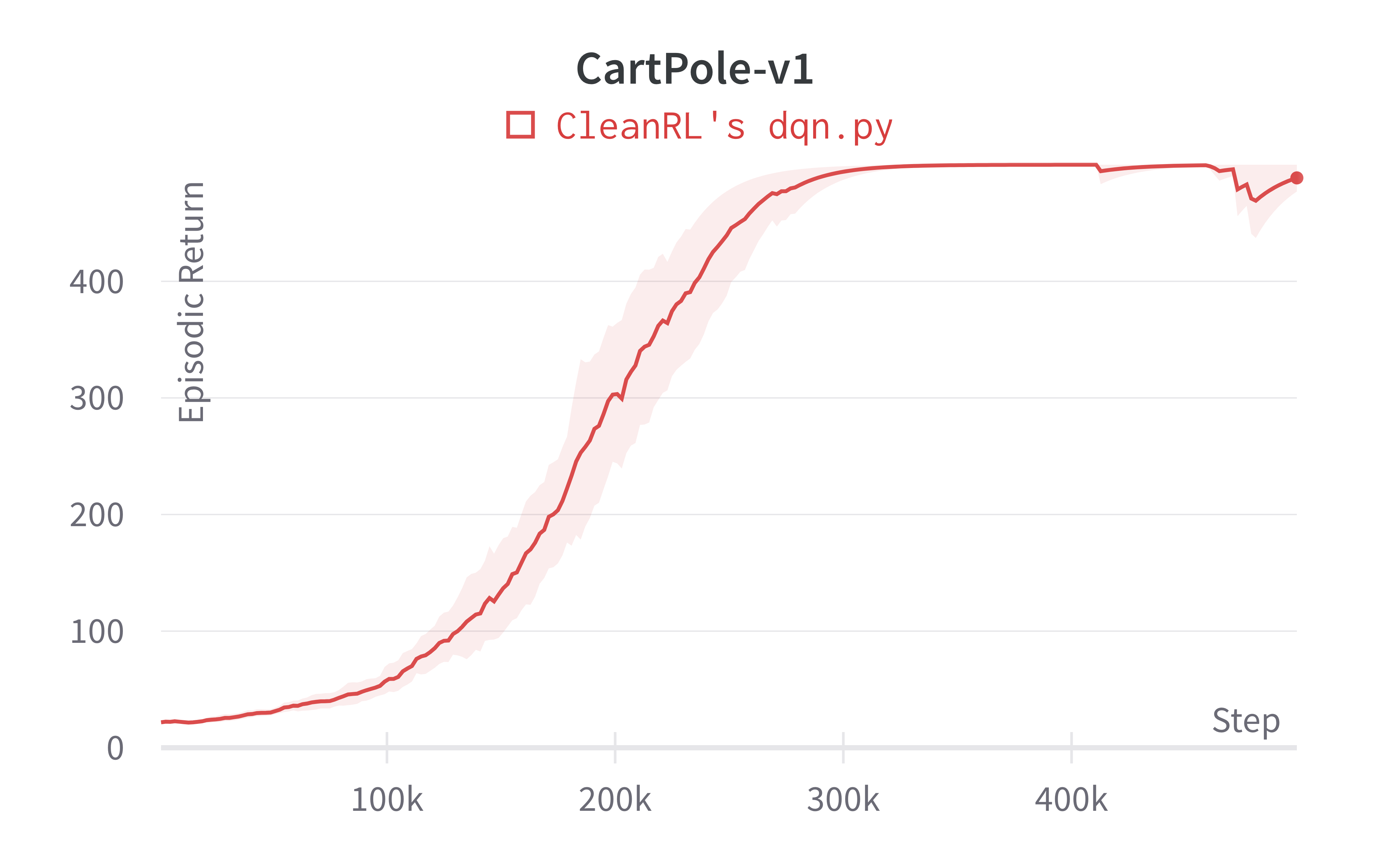

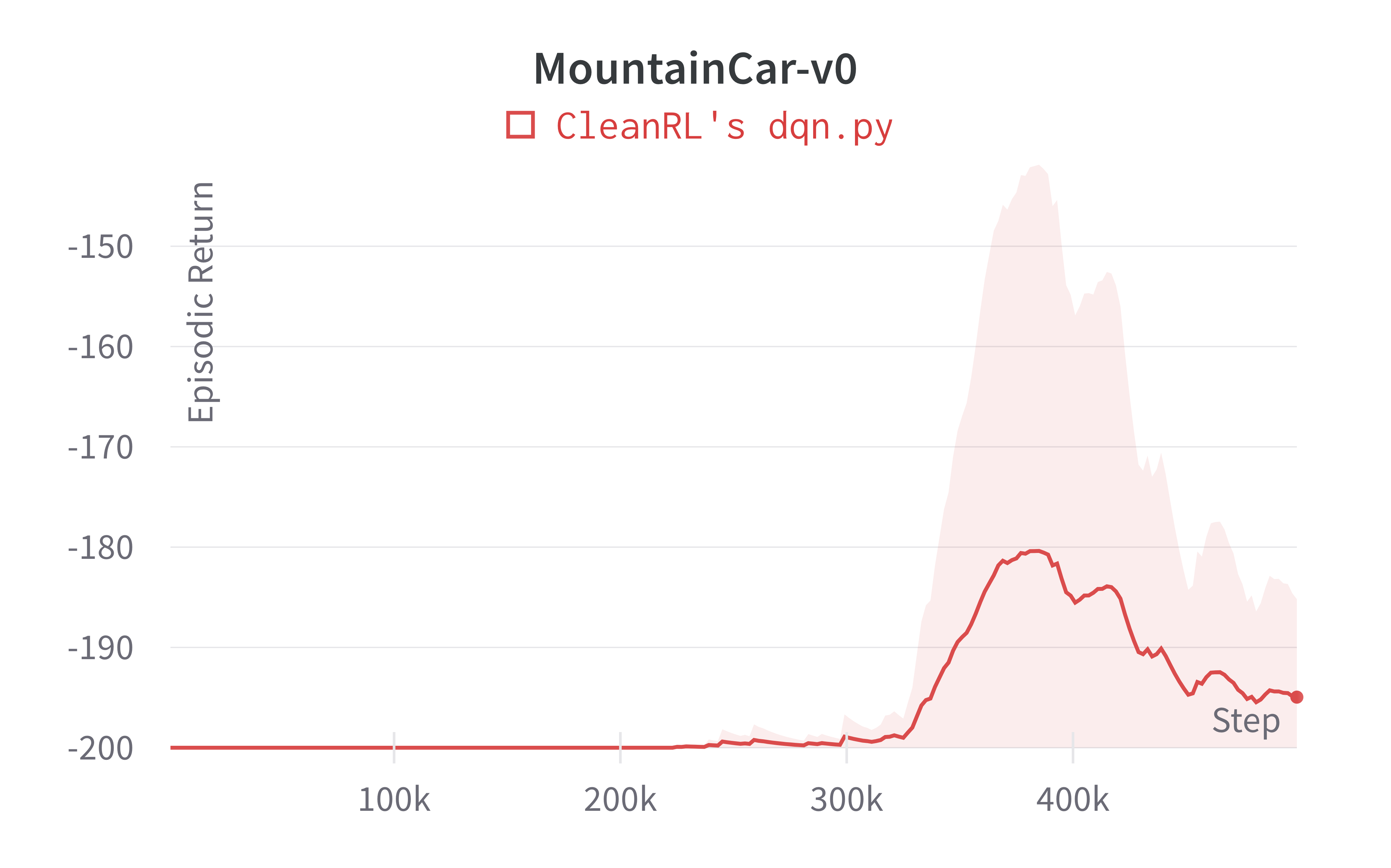
Tracked experiments and game play videos:
dqn_atari_jax.py
The dqn_atari_jax.py has the following features:
- Uses Jax, Flax, and Optax instead of
torch. dqn_atari_jax.py is roughly 25%-50% faster than dqn_atari.py - For playing Atari games. It uses convolutional layers and common atari-based pre-processing techniques.
- Works with the Atari's pixel
Boxobservation space of shape(210, 160, 3) - Works with the
Discreteaction space
Usage
poetry install --with atari,jax
poetry run pip install --upgrade "jax[cuda]==0.3.17" -f https://storage.googleapis.com/jax-releases/jax_cuda_releases.html
python cleanrl/dqn_atari_jax.py --env-id BreakoutNoFrameskip-v4
python cleanrl/dqn_atari_jax.py --env-id PongNoFrameskip-v4
Warning
Note that JAX does not work in Windows . The official docs recommends using Windows Subsystem for Linux (WSL) to install JAX.
Explanation of the logged metrics
See related docs for dqn_atari.py.
Implementation details
See related docs for dqn_atari.py.
Experiment results
To run benchmark experiments, see benchmark/dqn.sh. Specifically, execute the following command:
Below are the average episodic returns for dqn_atari_jax.py (3 random seeds).
| Environment | dqn_atari_jax.py 10M steps |
dqn_atari.py 10M steps |
(Mnih et al., 2015)1 50M steps | (Hessel et al., 2017, Figure 5)3 |
|---|---|---|---|---|
| BreakoutNoFrameskip-v4 | 377.82 ± 34.91 | 366.928 ± 39.89 | 401.2 ± 26.9 | ~230 at 10M steps, ~300 at 50M steps |
| PongNoFrameskip-v4 | 20.43 ± 0.34 | 20.25 ± 0.41 | 18.9 ± 1.3 | ~20 10M steps, ~20 at 50M steps |
| BeamRiderNoFrameskip-v4 | 5938.13 ± 955.84 | 6673.24 ± 1434.37 | 6846 ± 1619 | ~6000 10M steps, ~7000 at 50M steps |
Info
We observe a speedup of ~25% in 'dqn_atari_jax.py' compared to 'dqn_atari.py'. This could be because the training loop is tightly integrated with the experience collection loop. We run a training loop every 4 environment steps by default. So more time is utilised in collecting experience than training the network. We observe much more speed-ups in algorithms which run a training step for each environment step. E.g., DDPG
Learning curves:

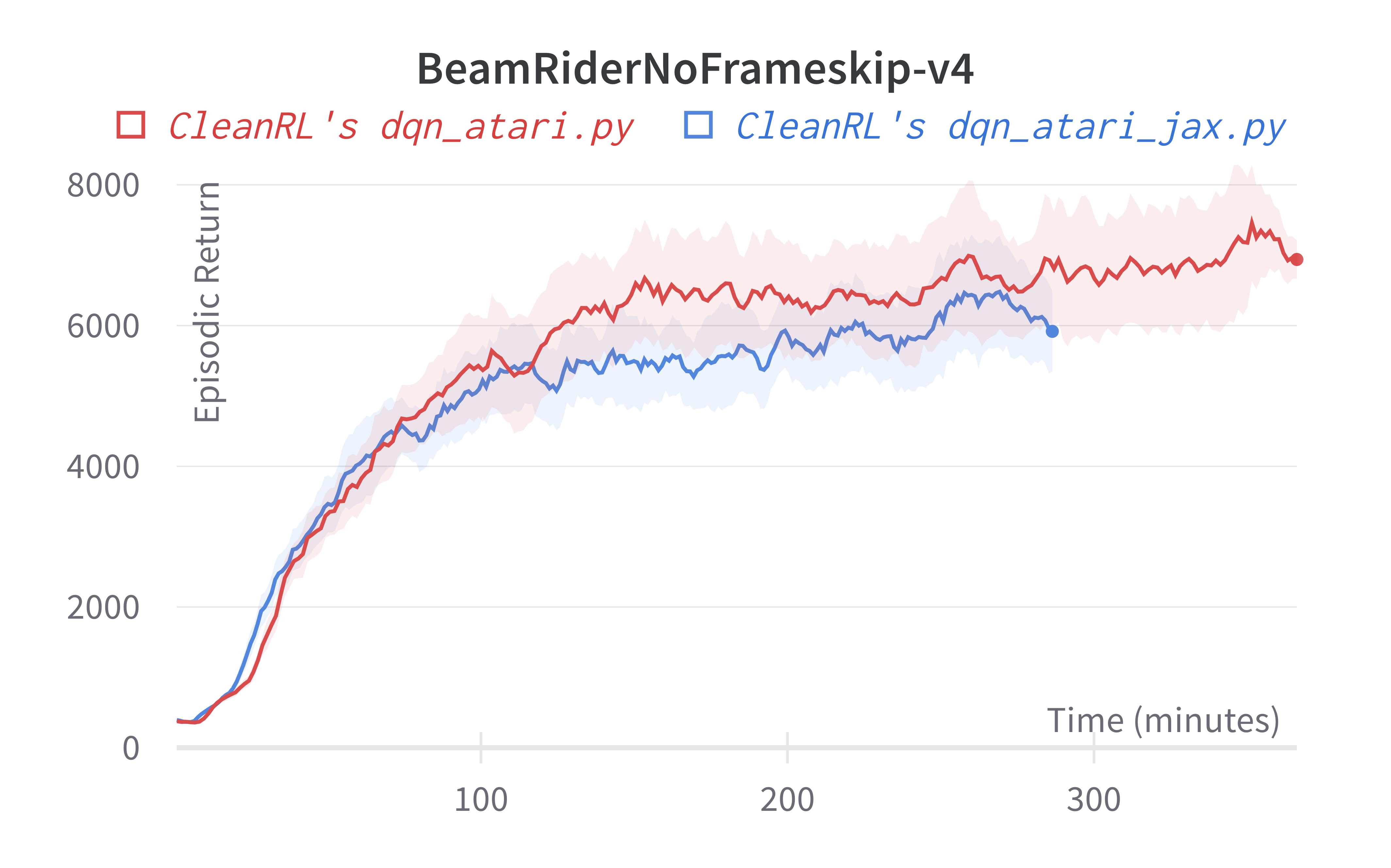
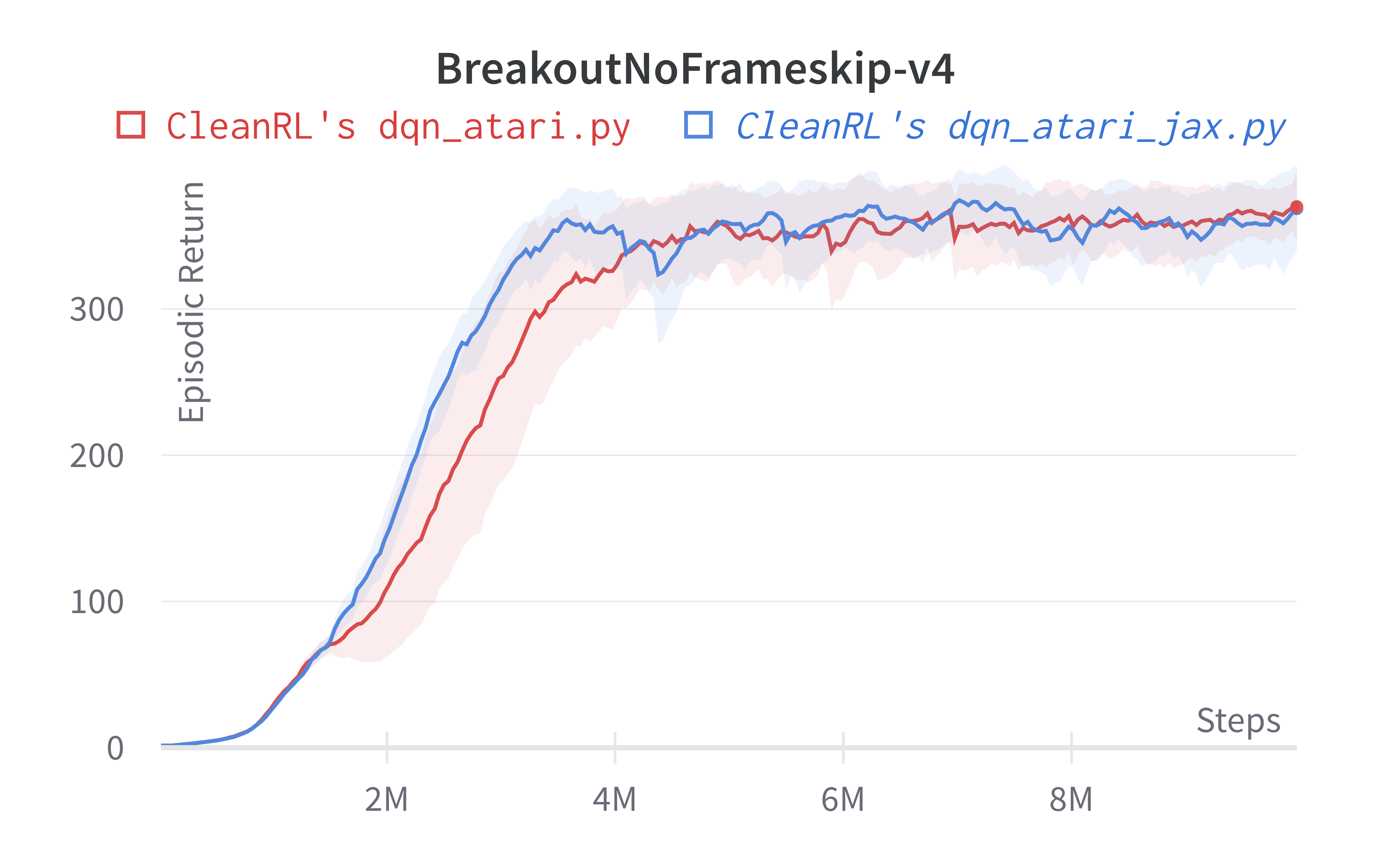
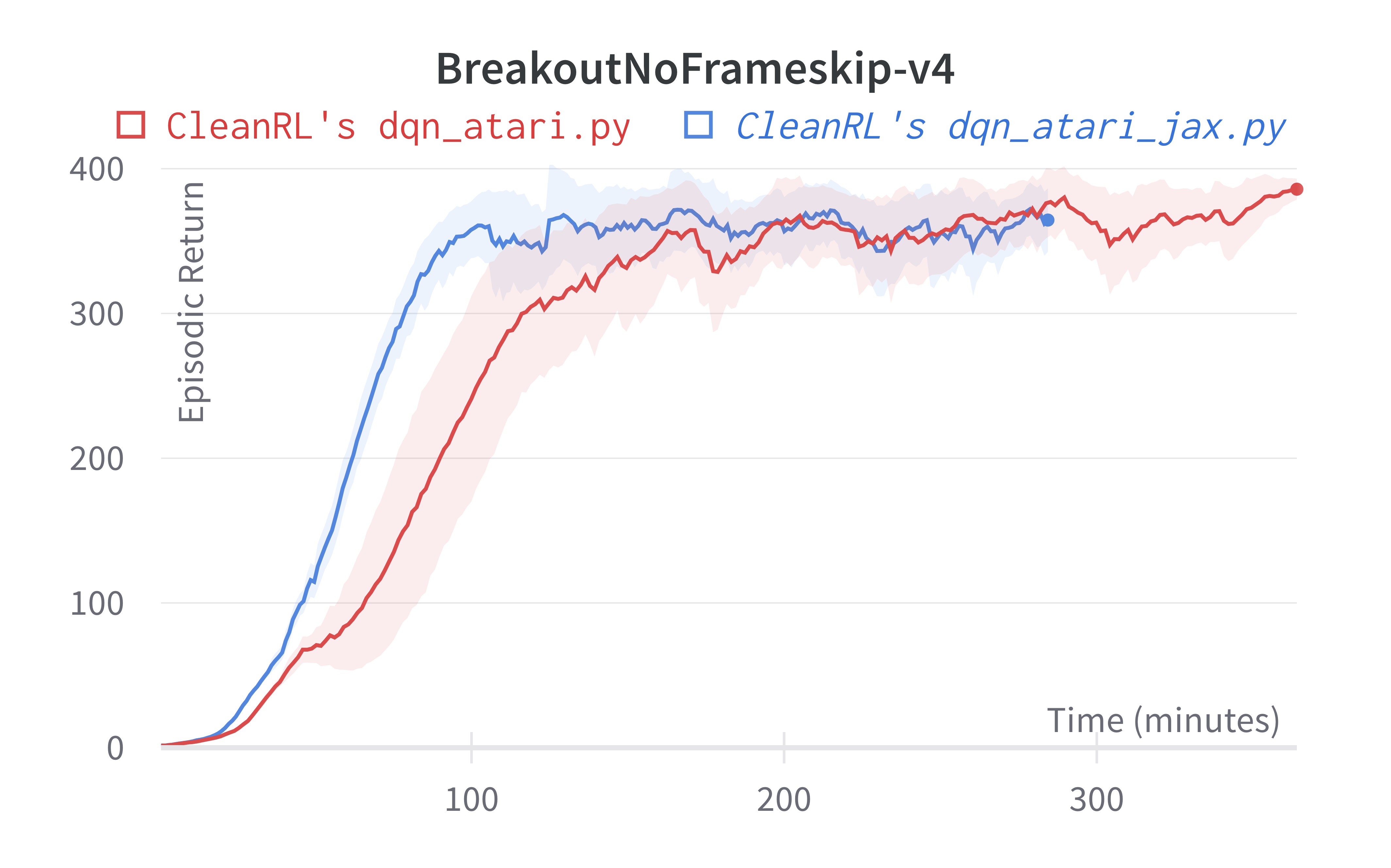

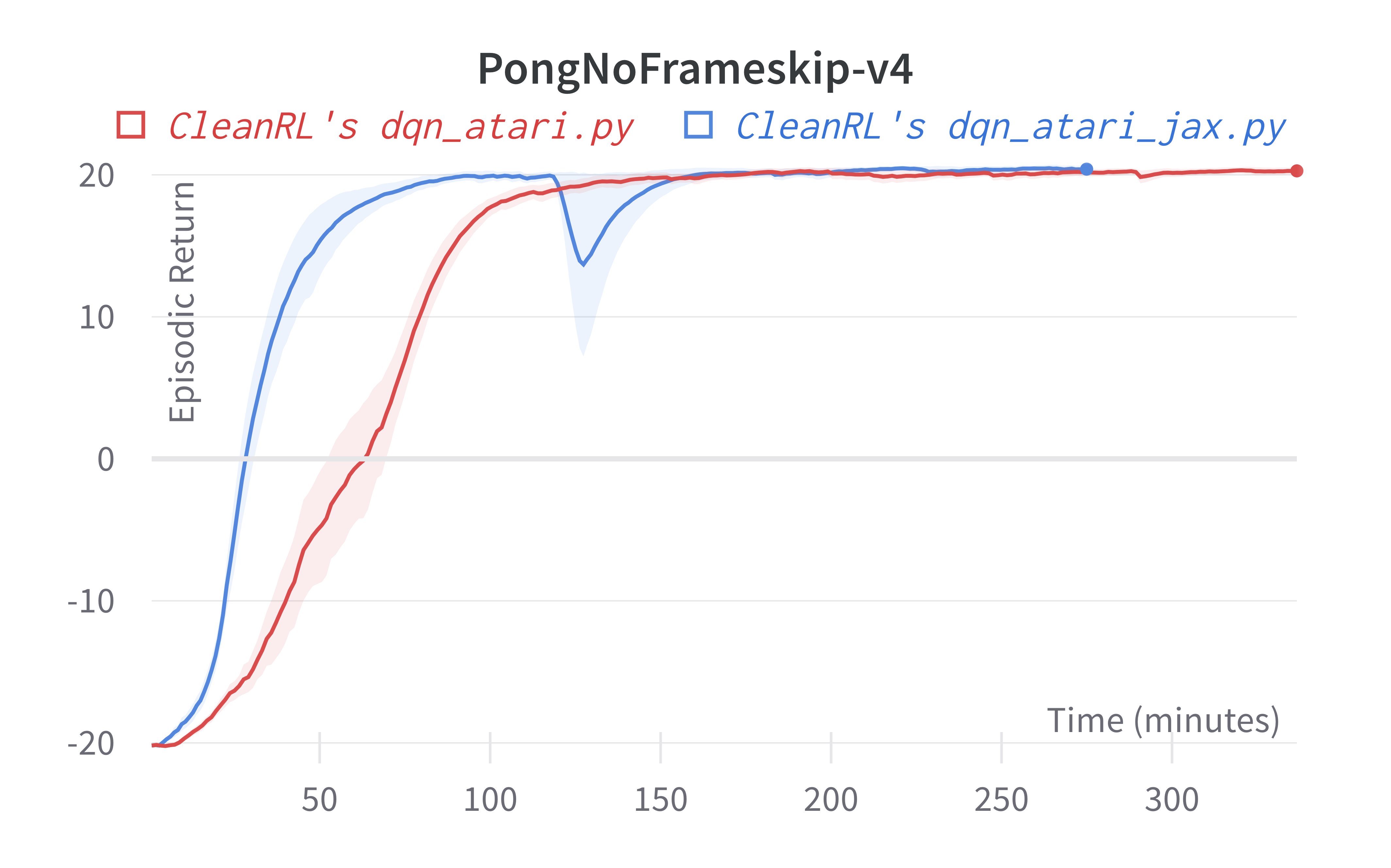
Tracked experiments and game play videos:
dqn_jax.py
- Uses Jax, Flax, and Optax instead of
torch. dqn_atari_jax.py is roughly 4% faster than dqn_atari.py - Works with the
Boxobservation space of low-level features - Works with the
Discreteaction space - Works with envs like
CartPole-v1
Usage
python cleanrl/dqn_jax.py --env-id CartPole-v1
Explanation of the logged metrics
See related docs for dqn_atari.py.
Implementation details
See related docs for dqn.py.
Experiment results
To run benchmark experiments, see benchmark/dqn.sh. Specifically, execute the following command:
Below are the average episodic returns for dqn_jax.py (3 random seeds).
| Environment | dqn_jax.py |
dqn.py |
|---|---|---|
| CartPole-v1 | 499.84 ± 0.24 | 488.69 ± 16.11 |
| Acrobot-v1 | -89.17 ± 8.79 | -91.54 ± 7.20 |
| MountainCar-v0 | -173.71 ± 29.14 | -194.95 ± 8.48 |
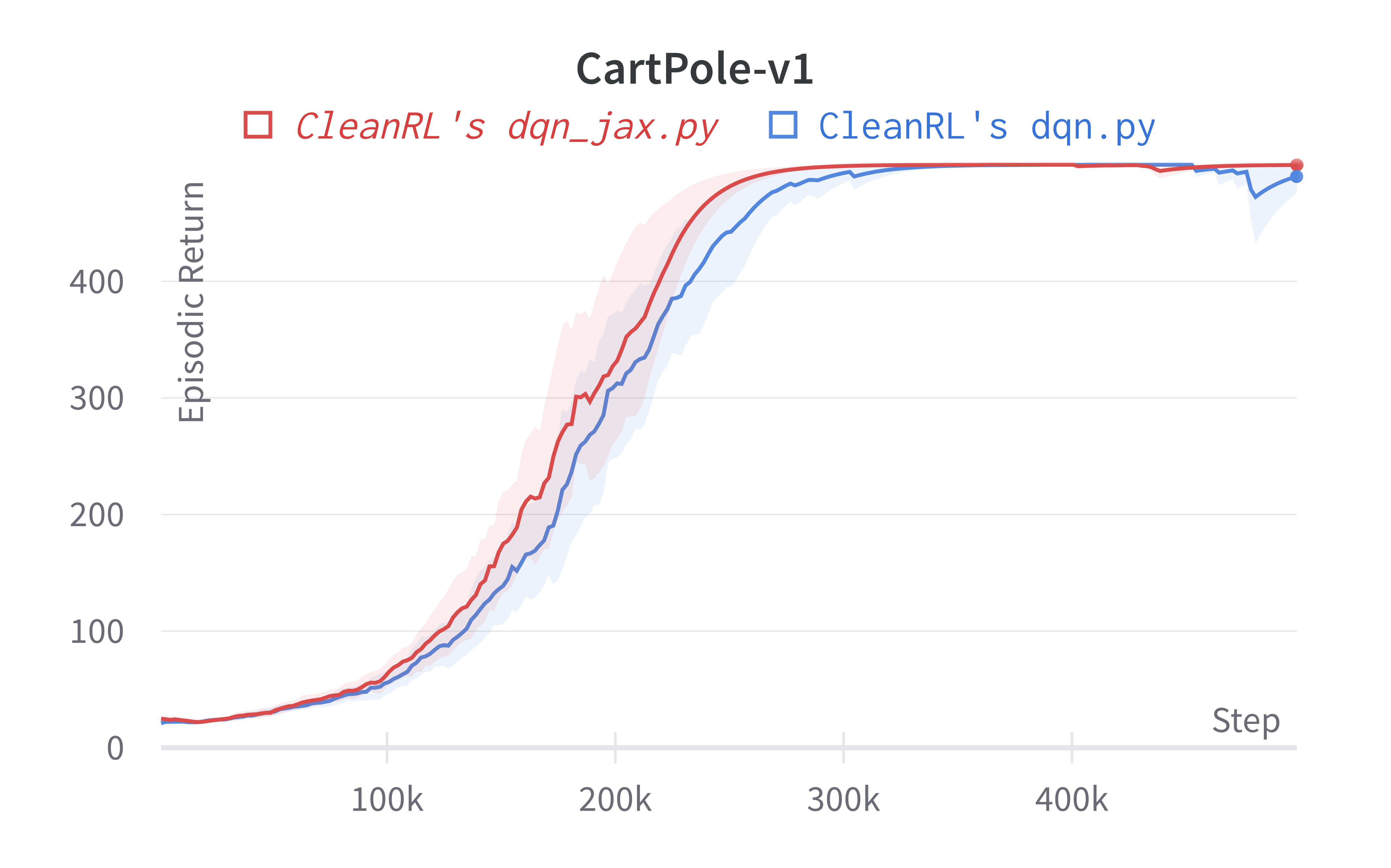
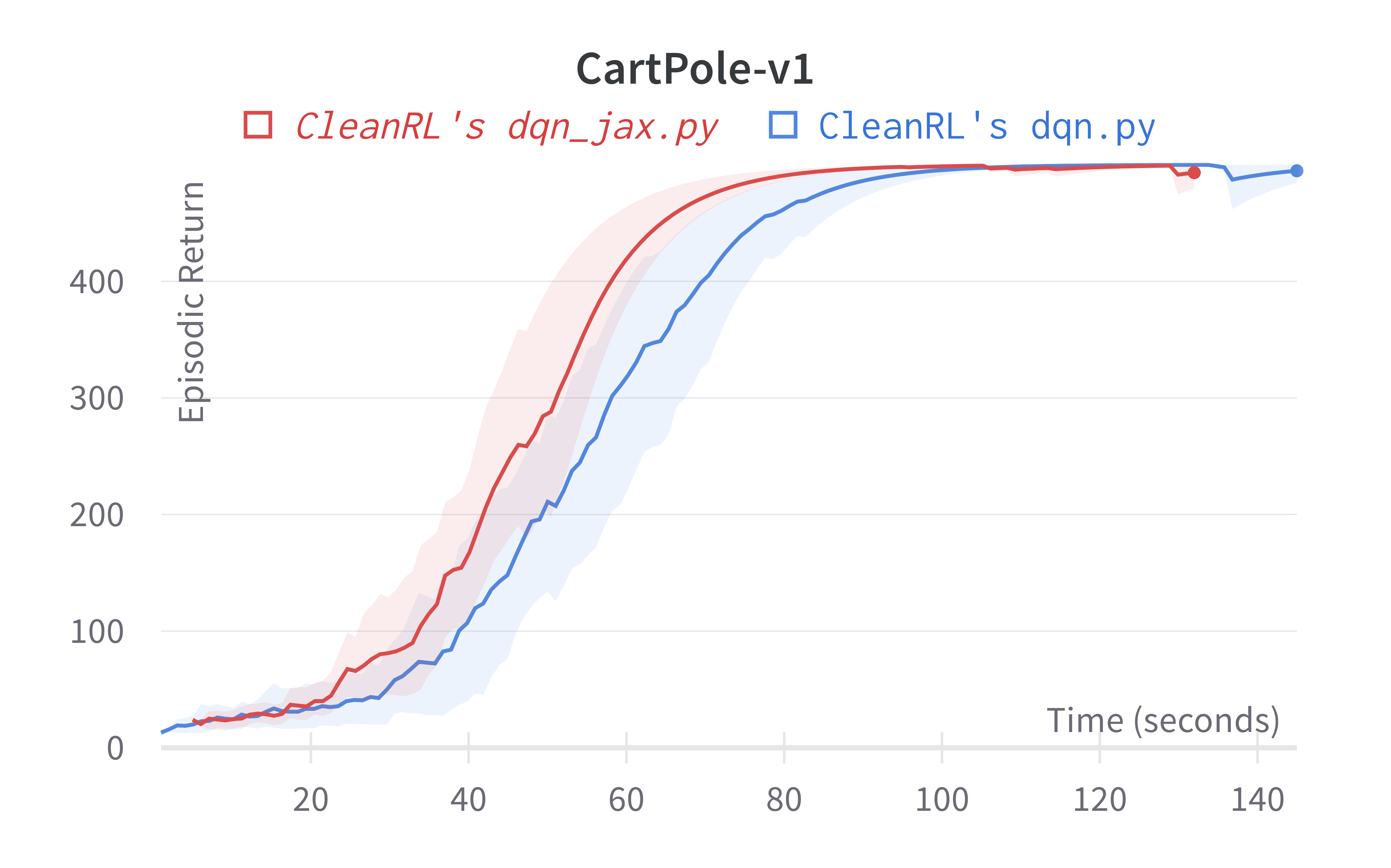
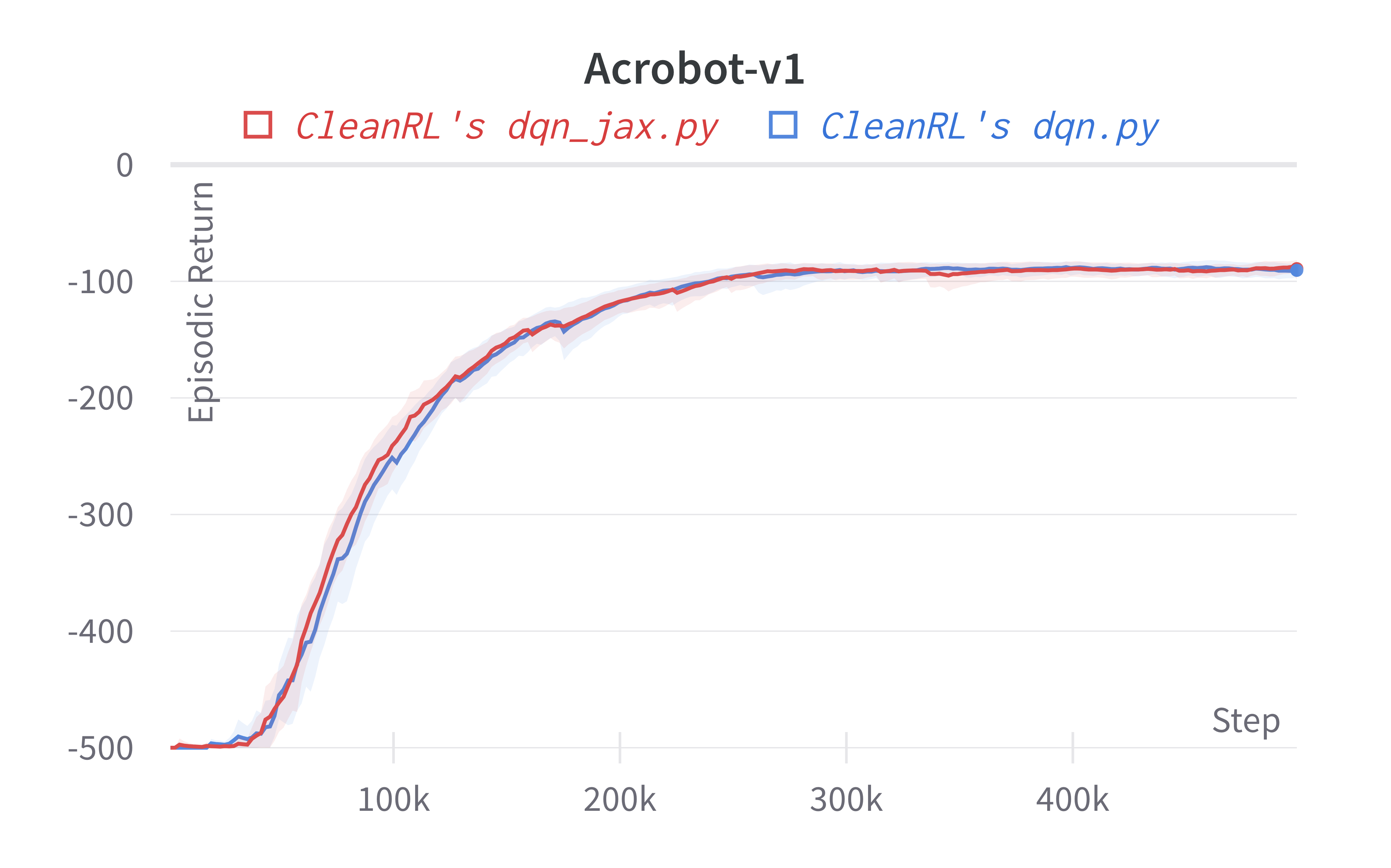

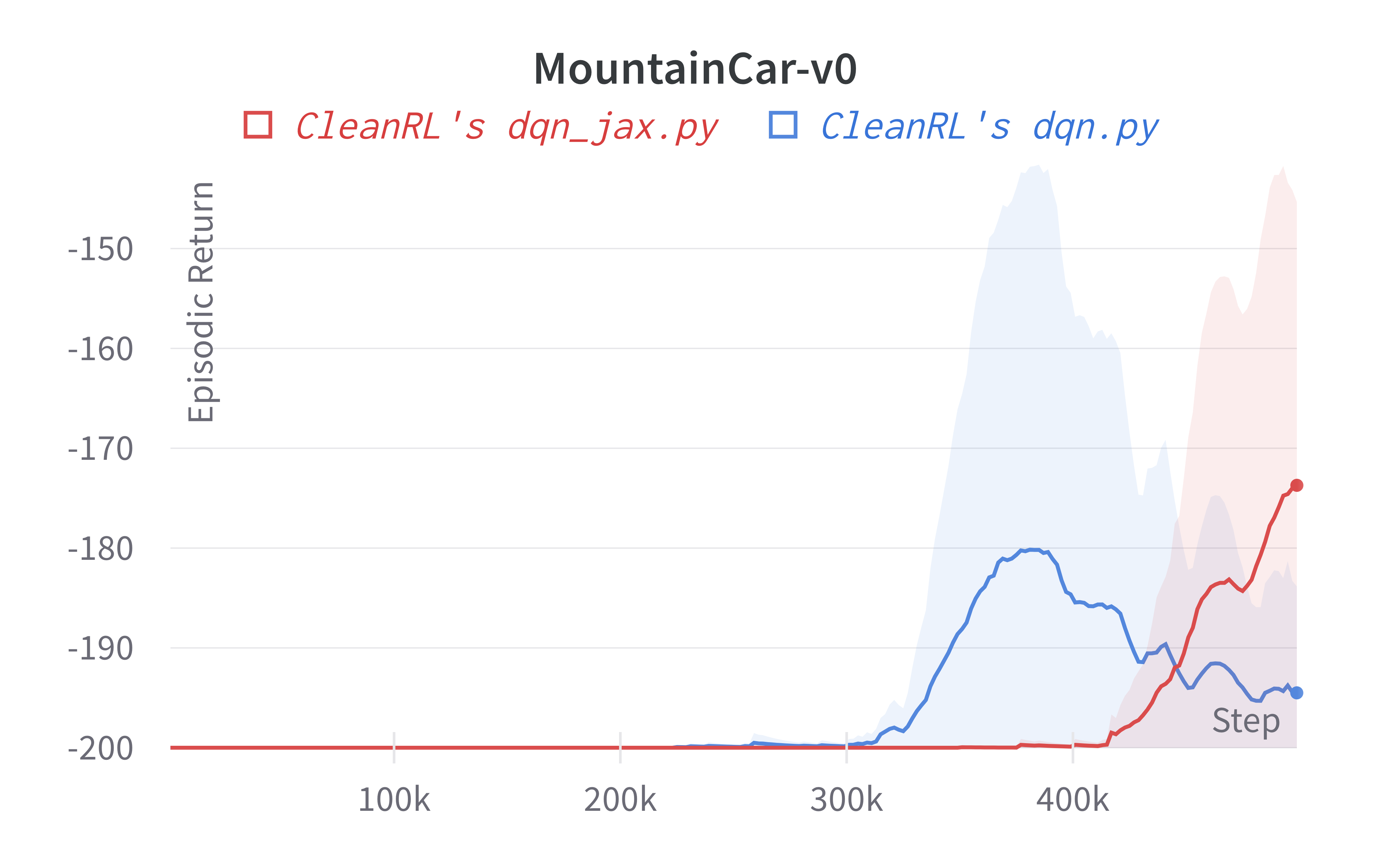
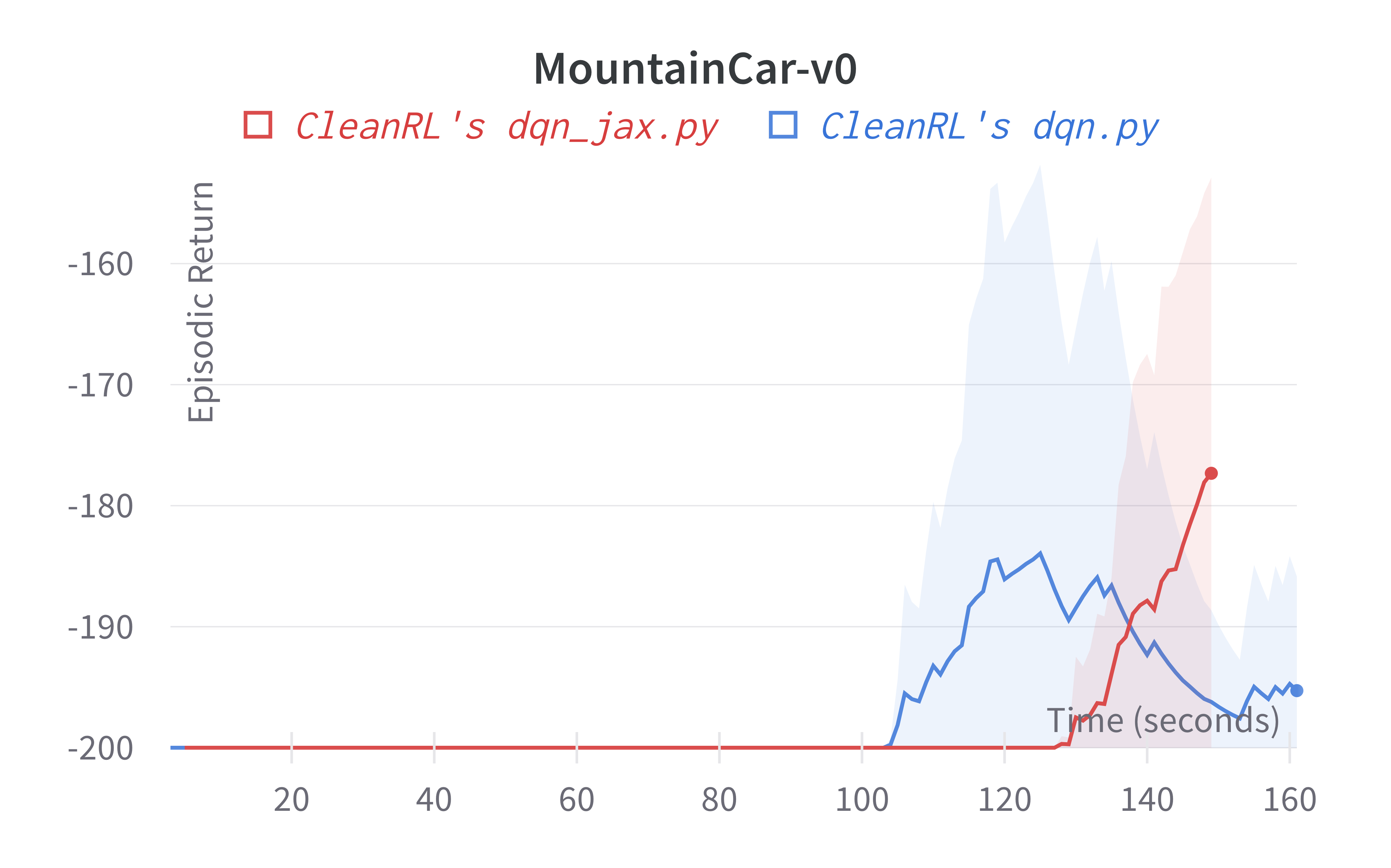
Tracked experiments and game play videos:
-
Mnih, V., Kavukcuoglu, K., Silver, D. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015). https://doi.org/10.1038/nature14236 ↩↩↩↩↩↩↩↩↩↩↩↩
-
[Proposal] Formal API handling of truncation vs termination. https://github.com/openai/gym/issues/2510 ↩
-
Hessel, M., Modayil, J., Hasselt, H.V., Schaul, T., Ostrovski, G., Dabney, W., Horgan, D., Piot, B., Azar, M.G., & Silver, D. (2018). Rainbow: Combining Improvements in Deep Reinforcement Learning. AAAI. ↩↩